Basic tutorial - Canopy hull method
This tutorial goes over the example code main_canopy_hull.m provided along the GitHub repository, and demonstrates the very basic usage of the canopy hull method.
Initialization
The code starts by clearing the workspace (were the variables are stored), closing all open figures, and adding the paths to subdirectories required in this demo.
% Clear all variables from the workspace and close all open figures
clear, close all
% Add the current directory and all the subdirectories to search path
addpath(genpath(pwd))
Defining the point cloud
The point cloud used as a basis for leaf generation in this tutorial is the example point cloud provided with the code repository of LeafGen. This is found in the example-data directory.
filename = 'example-data/examplePC.mat';
ptCloud = importdata(filename);
ptCloud = double(ptCloud);
The example point cloud is already stored as a MATLAB compatible .mat file, but it is also possible to read other types of point cloud files to MATLAB.
Defining leaf base geometry
The leaf base geometry is defined by setting the vertice points of the geometry and indicating the triangles with respect to the vertices. These values are assigned to the LeafProperties struct.
% Vertices of the leaf base geometry
LeafProperties.vertices = [0.0 0.0 0.0;
-0.04 0.02 0.0;
0.0 0.10 0.0;
0.04 0.02 0.0];
% Triangles of the leaf base geometry
LeafProperties.triangles = [1 2 3;
1 3 4];
In the LeafProperties.vertices matrix each row corresponds to a singe vertice point and in the LeafProperties.triangles each row contains the row indices of vertices used for the triangles. These matrices define a leaf geometry based on two triangles which looks like this:
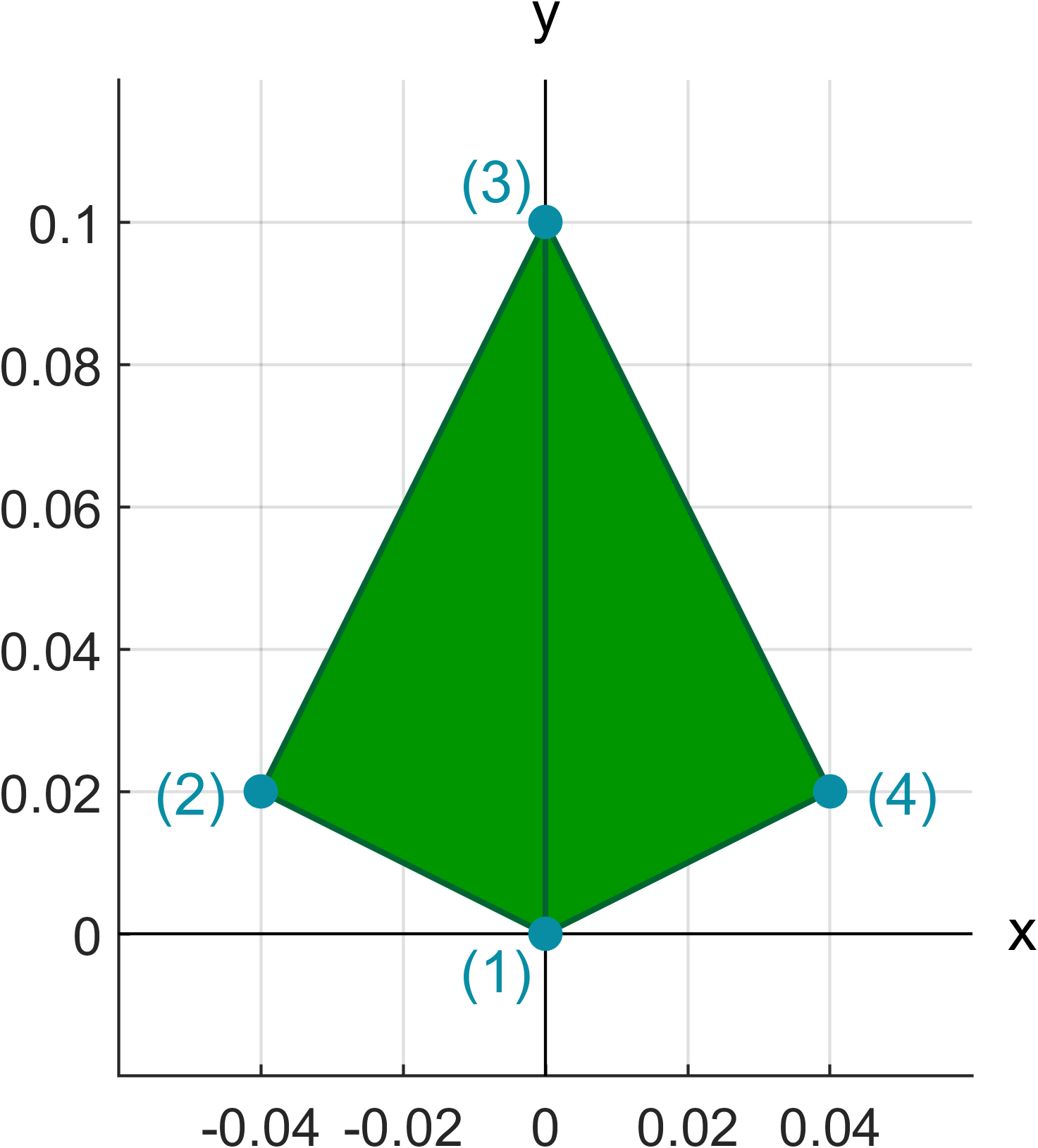
The absolute dimensions of the leaf base geometry are not important, since the base geometry is scaled to the correct size in the LSD sampling phase. Only the shape of the base geometry is preserved.
Defining target leaf distributions
The target distribution types and parameters for LADD, LOD, and LSD are defined in the TargetDistributions struct.
The LADD marginal distribution types and parameters with respect to the structural variables are defined as:
% LADD relative height
TargetDistributions.dTypeLADDh = 'beta';
TargetDistributions.pLADDh = [22 3];
% LADD relative branch distance
TargetDistributions.dTypeLADDd = 'weibull';
TargetDistributions.pLADDd = [3.3 2.8];
% LADD compass direction
TargetDistributions.dTypeLADDc = 'vonmises';
TargetDistributions.pLADDc = [5/4*pi 0.1];
Fields dTypeLADDh and pLADDh define the distribution type and parameters for the LADD marginal distribution on the relative height, in this case a beta distribution with parameters $\alpha$ = 22 and $\beta$ = 3. Similarly, dTypeLADDd and pLADDd define the relative branch distance marginal distribution as a truncated Weibull distribution with the scale parameter of $\lambda$ = 3.3 and the shape parameter of $k$ = 2.8, and dTypeLADDc and pLADDc define the compass direction marginal distribution as a von Mises distribution with the mean direction of $\mu = \frac{5\pi}{4}$ and the concentration parameter of $\kappa$ = 0.1.
The LOD marginal distribution types and parameters with respect to the inclination and azimuth angles of leaf normals are defined as:
% LOD inclination angle
TargetDistributions.dTypeLODinc = 'dewit';
TargetDistributions.fun_pLODinc = @(h,d,c) [1 2];
% LOD azimuth angle
TargetDistributions.dTypeLODaz = 'uniform';
TargetDistributions.fun_pLODaz = @(h,d,c) [];
The dTypeLODinc and fun_pLODinc fields define the distribution type for leaf inclination angle and the function for the distribution parameters, in this case a generalized de Wit’s distribution with parameters a = 1 and b = 2. The definition of distribution parameters, compared to LADD, is now done with a function, since the shape of LOD is allowed to change with respect to the structural variables. In this example, the parameters for inclination angle are set to be identical for the whole tree, so the field fun_pLODinc is set to be a handle for a constant function over all variable values. The dTypeLODaz and fun_pLODaz fields define the distribution type and parameters for the leaf azimuth angle, in this case a uniform distribution and thus an empty parameter function as no parameters are needed for uniform distribution on the azimuth angle (the distribution covers values from $0$ to $2\pi$ uniformly).
The LSD type and parameters, similarly to LOD, are defined as:
TargetDistributions.dTypeLSD = 'normal';
TargetDistributions.fun_pLSD = @(h,d,c) [0.004 0.00025^2];
The dTypeLSD and fun_pLSD fields define the distribution type and parameter function for the LSD, in this case a normal distribution with expected value of 40 square centimeters and a variance of 2.5$^2$ square centimeters.
The parameters of LOD inclination and azimuth angle distributions as well as LSD have to be given as function handles with three variables: relative height, relative branch distance, and compass direction. This holds even in the case they are constant or empty.
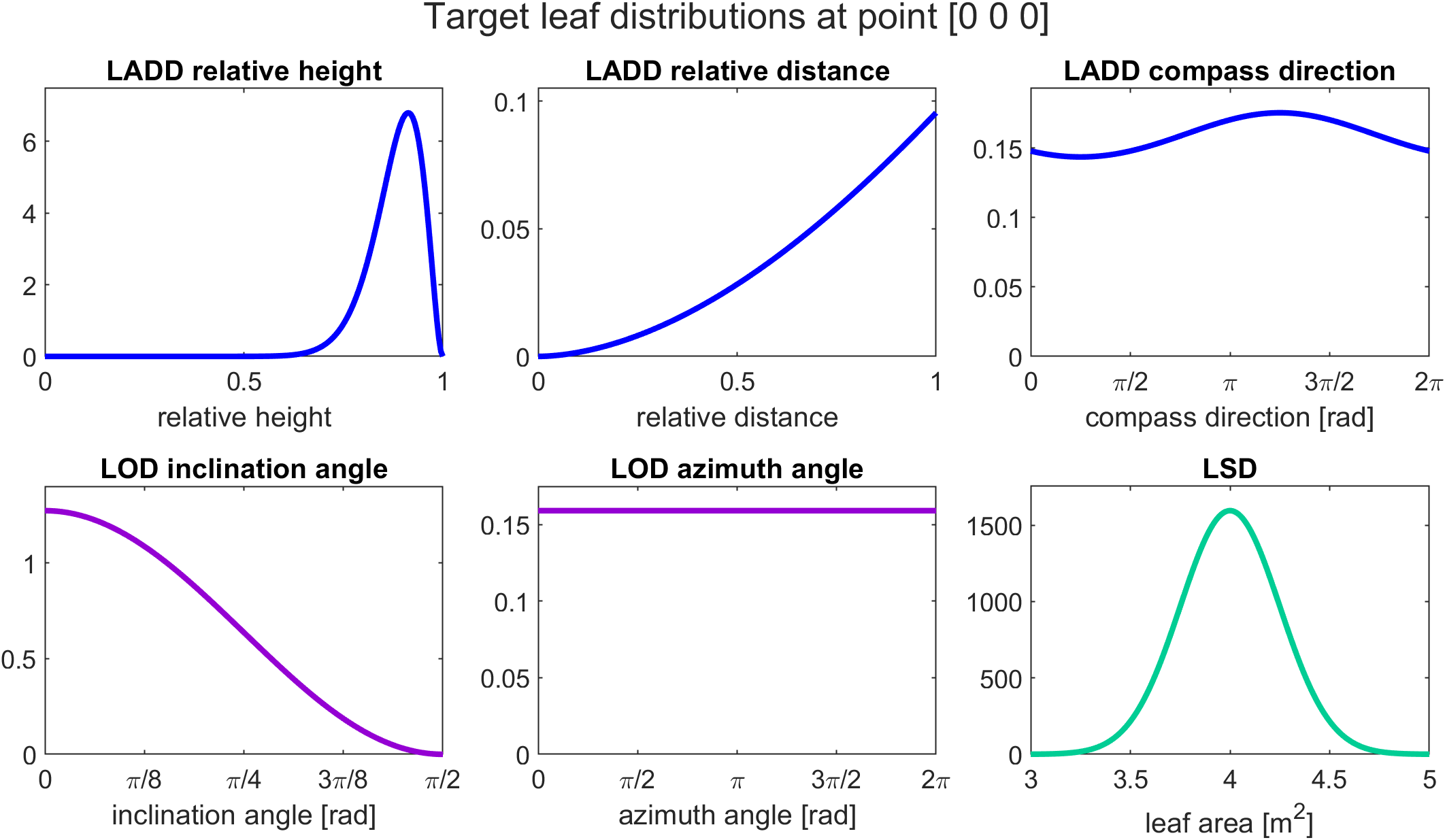
Before starting the leaf generation we can visualize the target distributions with the visualize_target_distributions function:
visualize_target_distributions(TargetDistributions,[0 0 0]);
The first input is the struct containing the distribution definitions and the second input is a vector for the structural variable coordinates of the point in which we want to visualize the distributions. In this case, all of our leaf distributions are stationary for the whole tree and do not vary depending on the structural variables, so we can put any point (in this case [0 0 0]) as the second input.
In the case of sructural-variable-dependent LOD or LSD, the shape of the distribution changes with respect to structural variable values. Therefore, when visualizing the target distributions, the user has to choose that for which part of the tree the distributions are visualized.
The visualization of the target distributions provides a figure showing the distributions we just defined above.
Setting stem coordinates
Before generating the foliage, we need to define what is considered to be the center of the tree stem. This information is needed to calculate the relative distance from stem as well as the compass direction, i.e., it is the reference center for the structural variables of the canopy hull. By default, LeafGen assumes the stem to be the vertical axis (z-axis). However, the tree of the example point cloud has a slight curve to it’s stem, so we need to adjust for this to make the foliage generation work better.
First we translate the point cloud such that the tree trunk is in the origin:
% Translate the lowest point of the cloud to the plane z=0
ptCloud = ptCloud - min(ptCloud(:,3));
% Translate the trunk of the tree to origin
tfBottom = ptCloud(:,3) < 1;
ptCloud = ptCloud - [mean(ptCloud(tfBottom,1:2)) 0];
Then we define stem coordinates which have been determined with visual inspection of the point cloud:
% Set the coordinates for the stem
stemCoordinates = [ 0 0 0;
0.47 -0.125 11.5;
0 0 max(ptCloud(:,3))];
The stem coordinates are defined such that the first row corresponds to the lowest stem coordinate (the origin) and the consecutive rows increase height-wise until the last row is the topmost point of the tree.
The stem coordinates define the reference center for the tree at each height. Therefore, even for trees with split stems or trees for which the actual stem ends before the top of the tree, one should define the stem coordinates such that they continue to the topmost part of the point cloud. This ensures there is a proper reference center for each height.
Setting target leaf area
The target leaf area is set in square meters to a variable named totalLeafArea:
totalLeafArea = 25;
The total leaf area can be essentially set to any positive value. In this case a total area of 25 square meters is chosen as the target. Larger values create larger foliage, which also increases the computational cost (mainly caused by the intersection prevention phase). If the value is too large the computation time can become very large as the overcrowding of leaves causes a lot of intersections. It is also possible that for too large total areas the target is not reached.
A realistic choice for the target leaf area can be derived, for example, by multiplying some realistic leaf area index (LAI) value with the ground projected area of the tree crown.
Generating foliage
The foliage is generated by calling the function generate_foliage_canopy_hull with the inputs defined above
[Leaves,aShape] = generate_foliage_canopy_hull(ptCloud, ...
TargetDistributions, ...
LeafProperties,totalLeafArea, ...
'StemCoordinates',stemCoordinates);
The stem coordinates is an optional input and therefore it is given with a name-value pair.
Visualizing the foliage and canopy hull in 3D
The generated foliage and the canopy hull can be visualized using the following code:
% Initialize figure
figure, clf
tiledlayout(1,2)
% Initialize first subplot
ax1 = nexttile;
% Plot point cloud
pc = aShape.Points;
plot3(pc(:,1),pc(:,2),pc(:,3),'k.','MarkerSize',1)
% Set subfigure properties
hold on, grid on, axis equal
xlabel('x')
ylabel('y')
zlabel('z')
% Plot alpha shape
plot(aShape,'FaceColor','m','FaceAlpha',0.2)
% Plot the defined stem
if exist('stemCoordinates','var')
plot3(stemCoordinates(:,1),stemCoordinates(:,2), ...
stemCoordinates(:,3),'c-','LineWidth',3);
else
pcTop = max(pc(:,3));
plot3([0 0],[0 0],[0 pcTop],'c-','LineWidth',3)
end
% Save the coordinate limits
xl = xlim;
yl = ylim;
zl = zlim;
% Initialize second subplot
ax2 = nexttile;
% Plot leaves
hLeaf = Leaves.plot_leaves();
% Set leaf color
set(hLeaf,'FaceColor',[0,150,0]./255,'EdgeColor','none');
% Set subfigure properties
grid on, axis equal, xlim(ax2,xl), ylim(ax2,yl), zlim(ax2,zl)
xlabel('x')
ylabel('y')
zlabel('z')
% Link the point of view for the subfigures
Link = linkprop([ax1, ax2],{'CameraUpVector', 'CameraPosition', ...
'CameraTarget', 'XLim', 'YLim', 'ZLim'});
setappdata(gcf, 'StoreTheLink', Link);
This produces a figure with two subplots:
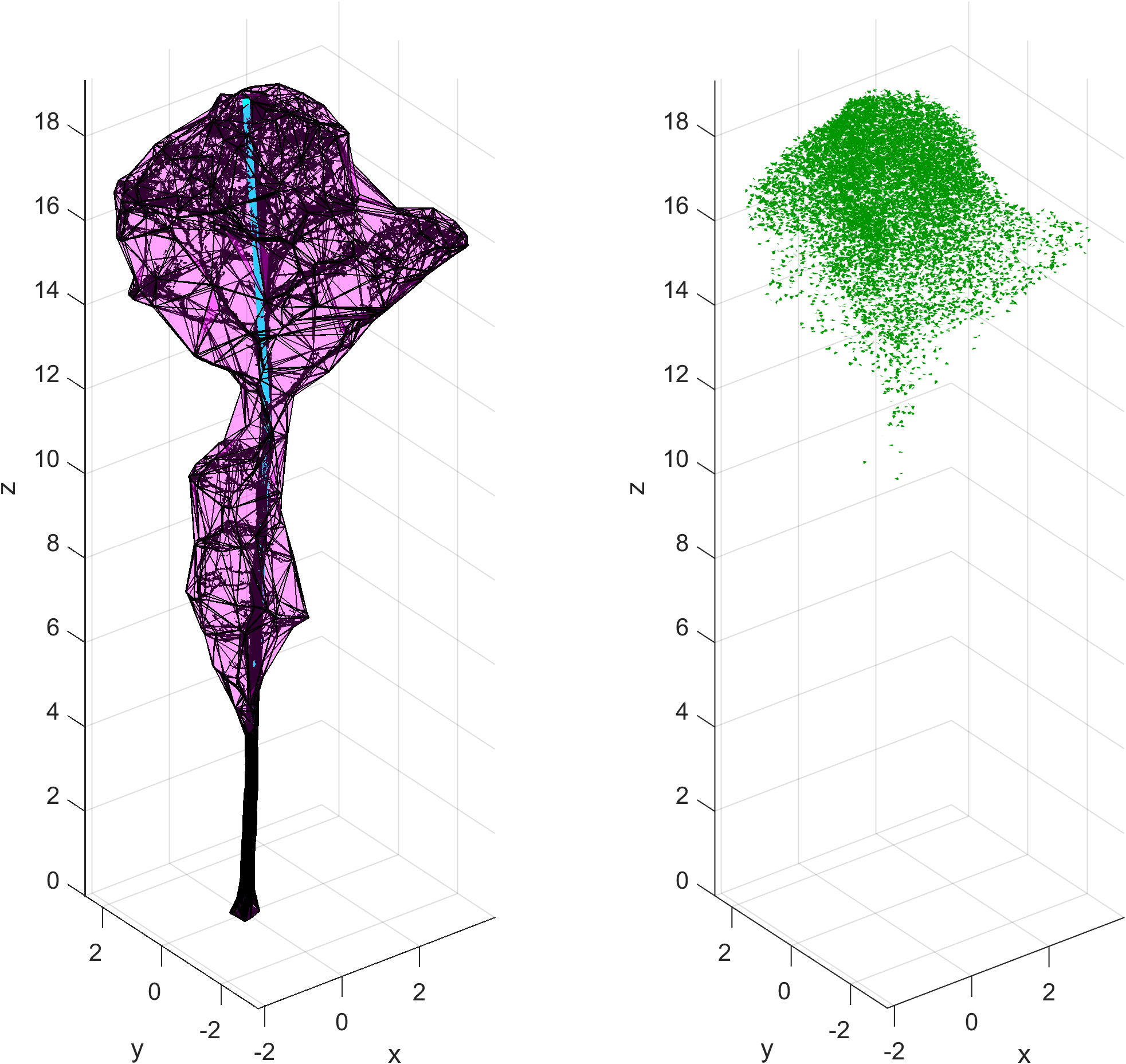
Here the alpha shape is visualized in magenta, point cloud in black, stem in cyan and the generated leaves in green.
Visualizing leaf distributions
The distributions of accepted leaves can be visualized with histograms.
LADD
The histograms of accepted leaf area with respect to each of the structural variables can be visualized alongside their target distributions with the following function calls:
plot_LADD_h_CH(aShape,Leaves,TargetDistributions);
plot_LADD_d_CH(aShape,Leaves,TargetDistributions, ...
'StemCoordinates',stemCoordinates);
plot_LADD_c_CH(aShape,Leaves,TargetDistributions, ...
'StemCoordinates',stemCoordinates);
Here, again, h refers to relative height, d refers to relative distance from stem (or tree centre), and c refers to compass direction.
LOD
The histograms of the inclination and azimuth angles of accepted leaves can be visualized with the following function calls:
plot_LOD_inc_CH(aShape,Leaves,'StemCoordinates',stemCoordinates);
plot_LOD_az_CH(aShape,Leaves,'StemCoordinates',stemCoordinates);
By default, these functions consider all leaves generated inside the point cloud, but they can be tuned to plot only specific intervals of the structural variables. In this tutorial the LOD for inclination and azimuth angles are stationary for the whole tree, so it makes sense to see the orientation histograms of all of the generated leaves.
LSD
The histogram of surface areas of accepted leaves can be visualized with the following function call:
plot_LSD_CH(aShape,Leaves,'StemCoordinates',stemCoordinates);
As with LOD, by default, this function considers all leaves generated within the point cloud, but it can be tuned to plot only specific intervals of the structural variables. In this tutorial also the LSD is stationary for the whole tree, so it makes sense to see the leaf size histogram of the whole tree at once.
Exporting to OBJ file
The generated foliage can be exported to a Wavefront OBJ file using a class function.
% Precision parameter for export
precision = 5;
% Exporting to obj file
Leaves.export_geometry('OBJ',true,'leaves_export.obj',precision);
The precision parameter defines the number of digits used when writing the geometry to an OBJ file: higher values give more precise geometry but increase the file size, whereas small values reduce the file size but provide less accurate geometry.